در سال ۲۰۱۲ "یان استوارت" تحقیقات گستردهی خود را به صورت کتابی به نام "در تعقیب ناشناختهها: ۱۷ معادلهای که دنیا را تغییر داد" منتشر کرد. در کتاب استوارت، اساسیترین معادلات ریاضی، جمعآوری شدهاند و بیشتر از بحثهای ریاضیوار، به جنبه و کاربرد آنها در زندگی انسان پرداخته شده است .
استوارت میگوید: "معادلات ریاضی گاهی خستهکننده و پیچیده به نظر میرسند و دلیلش هم این است که با روشهای پیچیده و خستهکنندهای بیان شدهاند."
او در ادامهی توضیحات خود اضافه میکند که ؛هر کسی میتوانداز زیبایی و اهمیت این معادلات قدردانی کند بدون این که روش حل آنها را بداند. هدف از معرفی این معادلات این است که جایگاه آنها را در زندگی انسان درک کنیم و از جنبههای ناگفته و پنهان آنها در تاریخ پرده برداریم."
وی خاطرنشان کرد:"این معادلات، بخش حیاتی و مهم فرهنگ ما هستند. چرا که هر کدام از آنها داستانی به همراه خود دارند. این داستانهای جذاب دربارهی افرادی است که آنها را کشف کردهاند و به نوعی شرایط زمانی آن دوران را بیان بازگو میکنند."
این ۱۷ معادله عبارت هستند از:
۱. قضیهی فیثاغورس
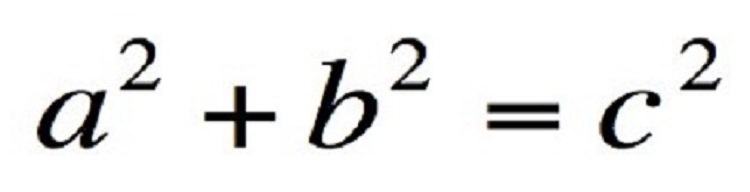
مفهوم: مربع وتر یک مثلث قائم الزاویه برابر با مجموع مربعات دو ضلع دیگر آن است.
تاریخچه: هر چند که کشف این قضیه به فیثا غورس نسبت داده شده است اما یافتهها حاکی از آن است که فیثا غورس اولین کسی نیست که این رابطه را اثبات کرده است. اولین فردی که میتوان کشف این قضیه را به او نسبت داد "اقلیدس" است. ضمن این که این احتمال وجود دارد که این قضیه توسط بابلیهای ۱۰۰۰ سال قبل از فیثا غورس هم کشف شده باشد.
اهمیت: این معادله، هندسه را با جبر پیوند میدهد و پایه و اساس علم "مثلثات" محسوب میشود. بدون در نظر گرفتن این معادله، مواردی مثل نقشهبرداری دقیق، نقشهسازی و مسیریابی، اموری غیرممکن بودند.
از منظر ریاضی محض، قضیهی فیثا غورس، در یک فضای اقلیدسی تعریف شده است. به عنوان مثال، این قضیه در مورد یک مثلث قائم الزاویه که بر روی سطح یک کره پخش شده است، صدق نمیکند.
کاربردهای مدرن: این روزها از روش "مثلثسازی" برای افزایش دقت مکانیابی در GPS استفاده میشود.
۲. معادلهی لگاریتمی
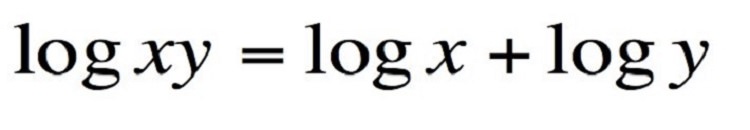
مفهوم: با این معادله میتوانید به وسیلهی عملیات حاصل جمع، اعداد را در هم ضرب کنید.
تاریخچه: مفهوم اولیهی این معادله توسط "جان نپر" که یک ملاک اسکاتلندی بود، کشف شد. او اکثر اوقات تلاش میکرد که اعداد بزرگ را در هم ضرب کند و این کار برای او وقتگیر و خستهکننده بود. بعدها "هنری بریگز" به منظور سادهسازی این محاسبات، جداول مرجعی را تنظیم کرد.
اهمیت: ظهور لگاریتم در ریاضیات منجر به یک انقلاب شد و محاسبات مهندسین و ستارهشناسان را سریعتر و سادهتر کرد. هر چند که با روی کار آمدن رایانهها این محاسبات سریعتر از قبل انجام میشوند اما این معادلات جایگاه خود را در میان معادلات بنیادین حفظ کردهاند.
کاربردهای مدرن: معادلات لگاریتمی و توابع نمایی در مدلسازی خیلی از فرآیندها مانند رشد بیولوژیکی و فروپاشی مواد رادیواکتیو استفاده میشوند.
۳. حساب دیفرانسیل (کلکول)
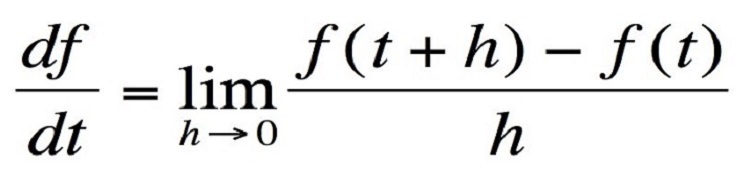
مفهوم: این معادلات کمک میکنند که نرخ تغییرات در هر لحظه محاسبه شود.
تاریخچه: معادلات حساب دیفرانسیل در اواخر قرن هفدهم، همزمان توسط "ایزاک نیوتون" و "گوتفرید لایبنیتس" تعریف شد. البته یک بحث و دعوای طولانی که کدام یک از آنها زودتر این رابطه را کشف کردهاند وجود داشت و هیچ وقت هم نتیجه ای از این مشاجرات حاصل نشد. بنابراین منطق حکم میکند که هر دو نفر به عنوان کاشفین این معادله در نظر گرفته شوند.
اهمیت: بنا به گفتهی استوارت: "این معادله بیشتر از این که یک تکنیک ریاضی باشد، نقش قابل توجهی در پیدایش دنیای مدرن ایفا کرده است."فهم حساب دیفرانسیل برای درک ما از اندازهگیریهای مربوط به منحنیها و سطوح، ضروری است. ضمن این که این معادلات مبنای خیلی از قوانین طبیعت هستند."
کاربردهای مدرن: کاربرد این معادلات در مسائل ریاضی که نیاز به پاسخ بهینه و مطلوب دارند لازم و ضروری است. علاوه براین از این معادلات در حل مسائل مربوط به پزشکی، اقتصاد، فیزیک، مهندسی و علوم رایانه استفاده میشود.
۴. قانون جهانی گرانش نیوتن
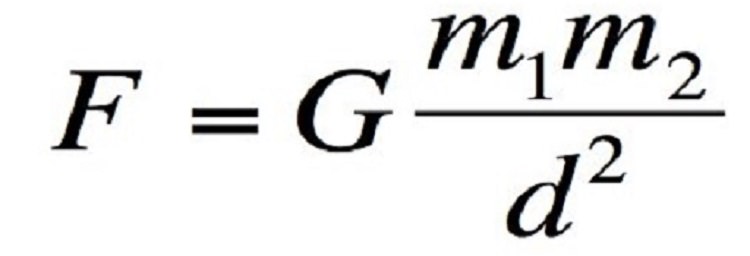
مفهوم: این رابطه، نیروی گرانش بین دو جسم را محاسبه میکند.
تاریخچه: ایزاک نیوتن قوانین خود را بر مبنای مطالعات "کپلر" که یک ستارهشناس آلمانی بود، استخراج کرده است. ضمن این که این احتمال وجود دارد که این قوانین را "رابرت هوک" کشف کرده باشد و نیوتن به یک سرقت علمی دست زده باشد.
اهمیت: قانون جهانی گرانش با استفاده از تکنیکهایی مثل معادلات دیفرانسیل میتواند وضعیت کلی دنیا را توضیح دهد. با این که بعدها قانون نسبیت انیشتین جانشین این قانون شد، هنوز هم در توضیحات علمی مربوط به تاثیرات برهمکنش اجرام فضایی مانند ستارگان، سیارات، فضاپیماهای ساختهی بشر، این معادله کاربرد دارد. امروزه از قانون جهانی گرانش برای طراحی مدارهای چرخش ماهوارهها و سفینهها هم استفاده میشود.
از نقطه نظر فلسفی، قانون نیوتن مهم است چرا که نیروی جاذبه را در همه جا محاسبه میکند. به بیانی دیگر، از توپی که به زمین میافتد تا تکامل کهکشانها، از این قانون پیروی میکنند.
کاربردهای مدرن: قوانین نیوتن با تئوریهای انیشتین تکمیل شد. قانون گرانش هنوز هم یک رابطهی کاربردی و مفید در مود اجرام فضایی محسوب میشود.
۵. اعداد مختلط
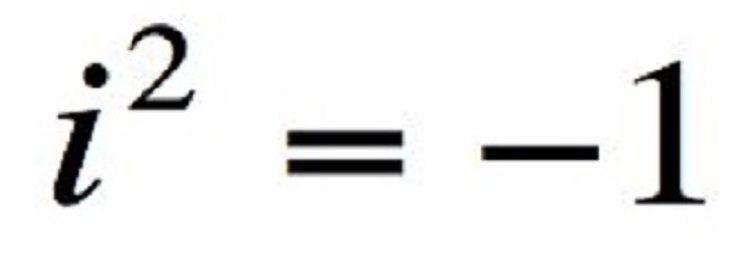
مفهوم: ریاضیدانها برای قابل قبول ساختن اعداد منفی زیر رادیکال، اعداد مختلط را معرفی کردند.
تاریخچه: اعداد موهومی یا مختلط توسط ریاضیدان و قمارباز معروف به نام "جرلامو کارنادو" کشف شد و سپس به وسیلهی افرادی چون "رافائل بامبلی" و "جان والیس" به شکل گستردهتری مطرح شد.این اعداد همچنان عجیب و غریب به نظر میآمدند تا این که "ویلیام همیلتون" آنها را تعریف کرد.
مبحث اعداد مختلط در ریاضیات بسیار جالب است. با معرفی اعداد مختلط دیگر تمام معادلات جبری جواب دارند. برای مثال معادله ای مثل x2 + 4 = 0 جواب حقیقی ندارد اما دارای ریشهی مختلط رادیکال ۴- یعنی ۲i است.
اهمیت: بنا به گفتهی استوارت: "... بیشتر فناوریهای مدرن، از روشنایی الکتریکی گرفته تا دوربینهای دیجیتال، بدون وجود اعداد مختلط هیچ گاه اختراع نمیشدند." توابع مشتقپذیر با مقادیر مختلط، شاخهای دیگر از ریاضیات به نام "آنالیز مختلط" را ایجاد کردند که فهم آن برای درک سیستمهای الکتریکی و انواع الگوریتمهای مدرن پردازش دادهها ضروری است.
کاربردهای مدرن: اعداد مختلط در مهندسی برق و نظریههای ریاضی استفادههای گستردهای دارند.
۶. قضیهی چندوجهی اویلر
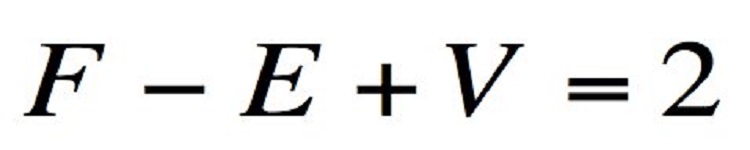
مفهوم: این قضیه یک رابطهی عددی را توضیح میدهد که دربارهی تمامی اشکال جامد از نوع خاص، صادق است.
تاریخچه: قضیهی چندوجهی اویلر توسط ریاضیدان بزرگ قرن هجدهم که "لئونارد اویلر" نام داشت، مطرح شد. همان طور که میدانیم چندوجهیها نسخهی سه بعدی از چندضلعیها هستند.
یک مکعب دارای ۸ راس، ۱۲ لبه و ۶ وجه است. اگر وجوه یک مکعب را از رئوس آن به هم بچسبانیم و لبهها را حذف کنیم، داریم: ۲=۱۲-۶+۸.
قضیهی اویلر برای چندوجهیهایی که حاصل جمع تفاضل لبهها از حاصل جمع رئوس و وجوه آنها ۲ باشد، قابل کاربرد است.
اهمیت: این قضیه اساس محاسبات مربوط به توپولوژی است.
کاربردهای مدرن: توپولوژی در فهم رفتار و عملکرد DNA به کار میرود و یک بخش اساسی از ابزارهای ریاضی برای درک شبکههای اجتماعی و اینترنت محسوب میشود.
۷. توزیع طبیعی
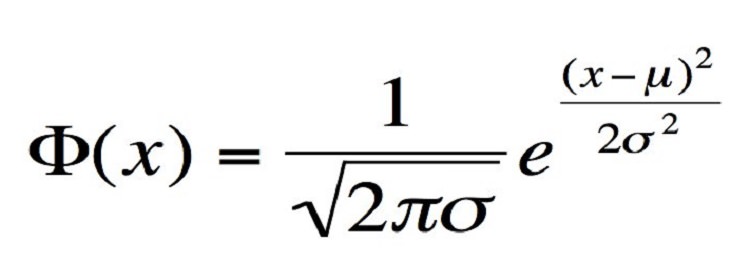
مفهوم: این رابطه یک توزیع طبیعی استادارد را تعریف میکند که به شکل یک نمودار زنگی شکل است و نشان میدهد که دادهها نسبت به میانگین تا چه اندازه انحراف دارند.
تاریخچه: قدم اولیهی ایجاد این نمودار توسط "بلز پاسکال" صورت گرفت اما بخش توزیع آن را برنولی به نتیجه رساند. در نهایت منحنی زنگی شکل فعلی که آن را در نمودارهای توزیع مشاهده میکنیم، حاصل کار ریاضیدان بلژیکی به نام "آدولف کوتله" است.
اهمیت: این معادله، پایه و اساس "آمار مدرن" را تشکیل میدهد. بدون آمار مدرن دیگر خبری از علوم اجتماعی نبود. طراحی آزمایشهای آماری، وابسته به نمودار توزیع طبیعی است و کمک میکند تا برای مدل کردن پارامترهای تصادفی از این نمودار استفاده شود.
کاربردهای مدرن: برای تعیین دز موثر دارو در مقاصد درمانی به کار میرود.
۸. معادلهی موج
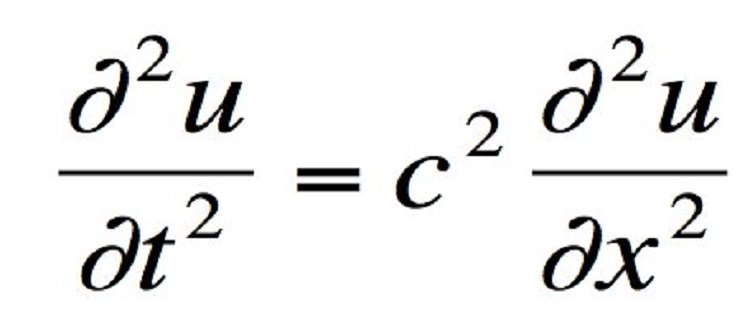
مفهوم: معادلهی موج یک معادلهی دیفرانسیلی است که رفتار امواج را توصیف میکند. برای نمونه میتوان رفتار ارتعاشی یک رشتهی ویولن را مثال زد.
تاریخچه: "دالامبر" و برنولی اولین ریاضیدانهایی بودند که در قرن هجدهم این رابطه را با کمی تفاوت کشف کردند.
اهمیت: رفتار موجی، به رخدادهای صوتی هم تعمیم داده شد. از این رو معادلهی موجی میتواند رفتارهایی مثل زمینلرزه و امواج اقیانوسها را توجیه کند.
کاربردهای مدرن: کمپانیهای نفتی با تنظیم مواد منفجره، دادههای حاصل از انقجار را از امواج صوتی استخراج میکنند تا ساختارهای زمینشناسی را پیشبینی کنند.
۹. تبدیل فوریه
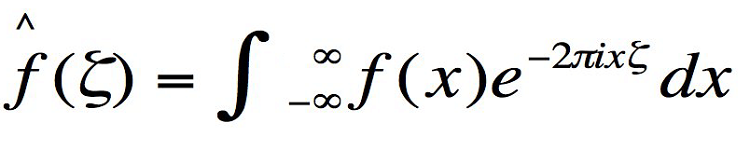
مفهوم: توصیف الگوهای زمانی به عنوان تابعی از فرکانس.
تاریخچه: "جوزف فوریه" این معادله را کشف کرد و از طریق راه حل معروف خود آن را به شکل یک معادلهی دیفرانسیل بسط داد که جریان حرارتی و معادلهی موج را در بر میگرفت.
اهمیت: این معادله برای الگوهای پیچیدهی موجی نظیر موسیقی، گفتار یا تصاویر نیز قابل استفاده است. این معادله در تحلیل و آنالیز بسیاری از انواع سیگنالها نیز کارآیی دارد.
کاربردهای مدرن: برای فشردهسازی اطلاعات تصاویر در قالب JPEG و کشف ساختارهای مولکولی از تبدیل فوریه استفاده میشود.
۱۰. معادلات ناویر-استوکس
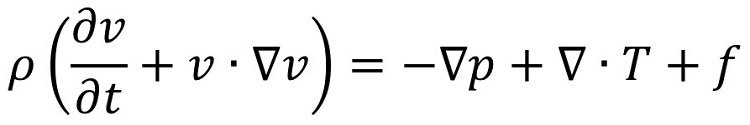
مفهوم: معادلات ناویر استوکس، پایه و اساس روابط مربوط به حرکت سیالات را تشکیل میدهد. سمت چپ معادله میزان تغییرات سرعت سیال بر حسب زمان را نشان میدهد و سمت راست آن به نیروهایی که بر سیال وارد میشود، دلالت دارد.
تاریخچه: لئونارد اویلر اولین کسی بود که حرکت سیالات را مدلسازی کرد. یک مهندس فرانسوی به نام "کلود-لوئی ناویر" به همراه "جرج استوکس" که یک ریاضیدان ایرلندی بود این مدلسازی را به شکل امروزی خود درآوردند.
اهمیت: از آنجا که رایانهها قدرت پردازش کافی برای حل تقریبی این معادلات را دارند، معادلات ناویر- استوکس جایگاه کارآمد و بااهمیتی در فیزیک پیدا کردهاند.از جملهی این کاربردها میتوان به ساخت وسایل نقلیهی آئرودینامیکی اشاره کرد.
هر چند که رایانههای مدرن با شبیه سازیهای تقریبی خود میتوانند پاسخ مفید و قابل قبولی را در مهندسی ارائه کنند اما پیدا کردن یک راه حل ریاضی که پاسخ دقیق را به ما بدهد همچنان به شکل یک صورت مسئلهی باز باقی مانده است و پیدا کردن راه حل آن، جایزهای معادل یک میلیون دلار را به همراه دارد!
کاربردهای مدرن: از این رابطه برای توسعهی جتهای مسافربری استفاده میشود.
۱۱. معادلات ماکسول
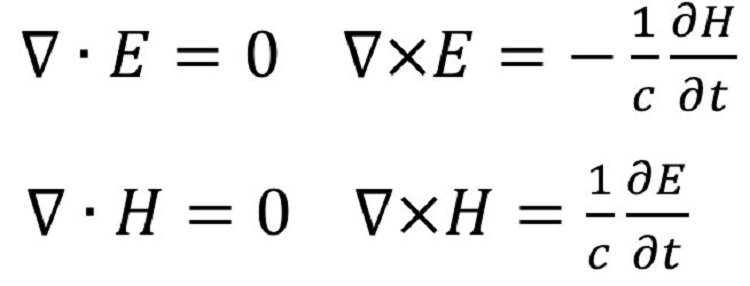
مفهوم: این معادلات بین پارامترهای الکتریکی و میدانهای مغناطیسی ارتباط برقرار میکنند.
تاریخچه: "مایکل فارادی" از اولین افرادی بود که به ارتباط بین الکتریسیته و مغناطیس پرداخت و "جیمز ماکسول" این روابط را به شکل معادله بازگو کرد.معادلات ماکسول در مواردی چون الکترومغناطیس کلاسیک، قوانین حرکت نیوتن و مکانیک کلاسیک کاربرد دارند.
اهمیت: با درک امواج الکترومغناطیسی، میتوان به مدرنترین فناوریهای مربوط به حوزهی برق و الکترونیک دست پیدا کرد.
کاربردهای مدرن: رادار، تلویزیون و وسایل ارتباطی مدرن از جمله کارآییهای مدرن معادلات ماکسول محسوب میشوند.
۱۲. قانون دوم ترمودینامیک
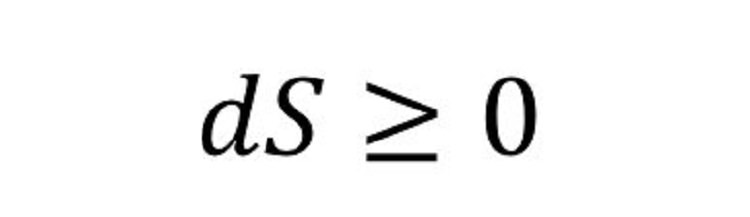
مفهوم: در تمام فرآیندهای ترمودینامیکی با اتلاف انرژی و گرما مواجه هستیم.
تاریخچه: "سعدی کارنو" نخستین کسی بود که فرضیهی "بازگشت ناپذیری فرآیندهای طبیعت" را مطرح کرد. پس ازآن ریاضیدانی به نام "لودویگ بولتزمن" این فرضیه را گسترش داد و "ویلیام تامسون" آن را به شکل رسمی اعلام کرد.
اهمیت: قانون دوم ترمودینامیک از طریق مفهوم انتروپی، درک صحیحی از انرژی و جهان هستی القا میکند. در واقع، میزان بینظمی یک سیستم توسط معیار انتروپی اندازهگیری میشود.اختلاف شرایط دمایی یکی از عواملی است که به افزایش بینظمی دامن میزند. برای مثال، سیستم گرمی که در مجاورت یک سیستم سرد قرار گرفته است تمایل دارد که گرما را به صورت خود به خود از سیستم گرم به سیستم سرد منتقل کند تا هر دو سیستم به تعادل برسند.
کاربردهای مدرن: ترمودینامیک ابزاری برای درک بهتر شیمی محسوب میشود و فهم آن برای شناخت ساختمان یک نیروگاه یا موتور الکتریکی ضروری است.
۱۳. نظریهی نسبیت انیشتین

مفهوم: انرژی و ماده، دو روی یک سکه هستند.
تاریخچه: پیدایش نظریهی نسبیت انیشتین بر پایهی آزمایشهای "آلبرت مایکلسون" و "ادوارد مورلی" صورت گرفت. مایکلسون و مورلی در یافتههای خود به این نتیجه رسیدند که حرکت نور از روش نیوتنی پیروی نمیکند و سرعت نور مستقل از سرعت منبع است.انیشتین این دیدگاه را در مقالات معروف خود در سال ۱۹۰۵ به صورت نسبیت خاص و در سال ۱۹۱۵ به صورت نسبیت عام منتشر کرد.
در نسبیت خاص، گذر زمان برای همهی افراد یکسان نیست و بستگی به میزان سرعت حرکت آنها دارد.
در نسبیت عام، نیروی جاذبه در فضایی به شکل یک منحنی خمیده شکل فرض میشود که به گذر زمان وابسته است. این نکته اولین تغییر عمدهای است که نسبت به قانون نیوتن مشاهده میشود. فهم نسبیت عام برای درک بهتر منشاء، ساختار و سرنوشت نهایی جهان مادی ضروری است.
اهمیت: این معادله، تقریبا معروفترین معادلهی تاریخ محسوب میشود که توانسته است نگرش ما را نسبت به ماده به طور کامل تغییر دهد.
کاربردهای مدرن: از این معادله برای مسیریابی GPS و ساخت سلاحهای هستهای استفاده میشود.
۱۴. معادلهی شرودینگر
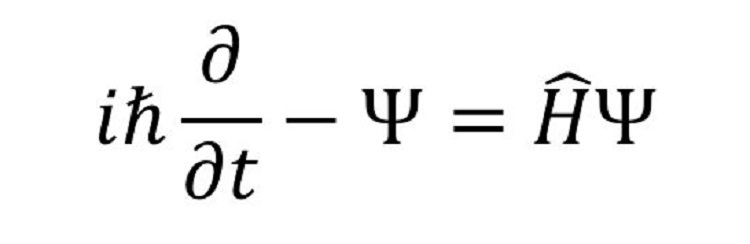
مفهوم: معادلهی شرودینگر یکی از بنیادیترین معادلات علم فیزیک به شمار میرود. در این مدل برای ماده، ماهیت موجی نسبت به ماهیت ذرهای ارجحیت دارد.
تاریخچه: "لویی-دوبروی ویکتور" در سال ۱۹۲۴ کشف کرد که ماده، ماهیتی دوگانه دارد. معادلهی شرودینگر در سال ۱۹۲۷ توسط "اروین شرودینگر" منتشر شد. این معادله سامانهی حرکت ذرات اتمی و ریزاتمی را در طول گذر زمان توصیف میکند.
اهمیت: معادلهی شرودینگر منجر به وقوع یک انقلاب در مقیاسهای کوچک فیزیکی شد.
مکانیک کوانتومی مدرن و نظریهی نسبیت عام، از موفقترین نظریههای علمی در طول تاریخ محسوب میشوند. تمام مشاهدات تجربی دنیای پیرامون ما با نتایج حاصل از این معادلات سازگاری کامل دارند.
کاربردهای مدرن: مکانیک کوانتومی در مدرن ترین فناوریها مانند انرژی هستهای، رایانههای ساخته شده از مواد نیمه رسانا، لیزرها و تمام پدیدههای کوانتومی حضور پررنگی دارد.
۱۵. نظریهی اطلاعات
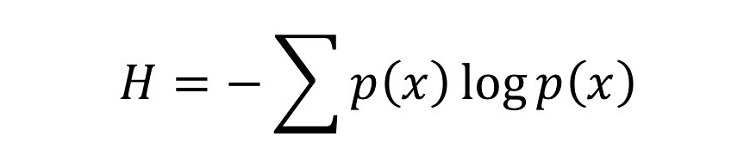
مفهوم: در این نظریه، اطلاعات حاصل از یک کد که شامل دادهها و علائم احتمالی است، برآورد خواهد شد.
تاریخچه: پس از جنگ جهانی دوم، این نظریه توسط "کلود شانون" در آزمایشگاه معتبر Bell Labs مطرح شد.
اهمیت: شانون مفهوم انتروپی اطلاعات را به عنوان یک معیار برای میزان تردید در رسیدن به یک مفهوم تلقی کرد. با در نظر گرفتن این فرض، اطلاعات محتواهایی مانند یک کتاب، ارسال یک تصویر با فرمت JPEG بر روی اینترنت و یا هر مورد دیگری قابل اندازهگیری است. انتروپی شانون نشان میدهد که چگونه بدون از دست دادن محتوا، میتوان آن را فشردهسازی کرد.
استفادهی مدرن: نتابج حاصل از اندازه گیریهای انتروپی شانون، منجر به شکلگیری مرکز اصلی شبکههای ارتباطی شد.
۱۶. الگوی لجستیک برای رشد جمعیت
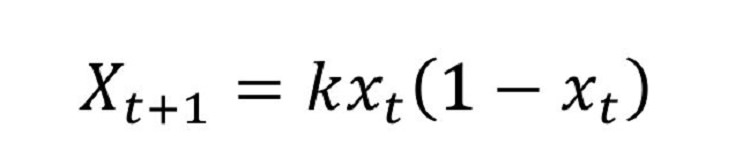
مفهوم: این الگو نشان میدهد که رشد جمعیت یک گونه محدود به منابع حیاتی است. نکتهی مهمی که در مورد این تابع وجود دارد، این است که پاسخهای آن میتواند به آشوب منجر شود و پاسخهای بی نهایت به دست بیایند.
تاریخچه: در سال ۱۹۷۵ "رابرت می" نخستین فردی بود که این مدل را در ارتباط با رشد جمعیت معرفی کرد.
اهمیت: با توسعهی فرضیهی آشوب، دیدگاه ما نسبتا به این گونه مسائل کاملا تغییر پیدا کرد و باعث شد که در راه حل آنها به صورت سیستمهای طبیعی عمل شود.
تئوری آشوب برای خیلی از ما شناخته شده است و مثال کلاسیک آن را میتوان وضعیت آب و هوا دانست. به این ترتیب که حرکت بال پروانه در یک قاره میتواند باعث بروز طوفان در قارهی دیگر شود.
کاربردهای مدرن: از این الگو برای مدل کردن زلزله و شرایط آب و هوایی استفاده میشود.
۱۷. مدل بلک- شولز
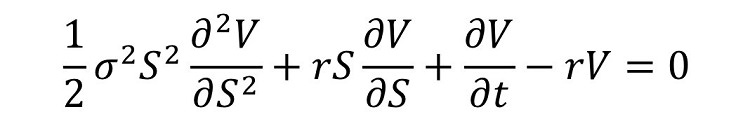
مفهوم: قراردادها، مرسوم ترین ابزارهای مالی محسوب میشوند. از این رو با افزایش تقاضا برای این ابزار مالی، مسئلهی قیمت گذاری قراردادها جایگاه بسیار مهمی در اقتصاد دارد. ارائهی مدل بلک-شولز در سال ۱۹۷۳، معادلات دیفرانسیل جزئی را بیش از پیش در زمینهی اقتصاد مورد توجه قرار داد. بنابراین برای تعیین قیمت این قراردادها نیاز به روشی ساده ودقیق برای حل این معادلات دیفرانسیل است.
تاریخچه: این معادله توسط "فیشر بلک" و " میرن شولز" مطرح شد و توسط "رابرت مرتون" توسعه پیدا کرد. بعدها جایزهی نوبل این کشف به هر سه نفر اهدا شد. هر چند که در زمان اهدای جایزه، دو سال از فوت فیشر بلک گذشته بود.
اهمیت: این مدل، هم اکنون توانسته است که بازار مشتقات چند تریلیون دلاری را برپا کند. البته اختلاف نظرهایی وجود دارد که استفاده از این معادله، باعث ایجاد بحرانهای مالی نیز شده است. در واقع این معادله، مفروضاتی دارد که در بازارهای مالی واقعی صادق نیستند.
کاربردهای مدرن: حتی بعد از وقوع بحرانهای مالی، باز هم از این معادله برای قیمتگذاری مشتقات استفاده میشود.